- Research Article
- Open access
- Published:
Parallel Backprojection: A Case Study in High-Performance Reconfigurable Computing
EURASIP Journal on Embedded Systems volume 2009, Article number: 727965 (2009)
Abstract
High-performance reconfigurable computing (HPRC) is a novel approach to provide large-scale computing power to modern scientific applications. Using both general-purpose processors and FPGAs allows application designers to exploit fine-grained and coarse-grained parallelism, achieving high degrees of speedup. One scientific application that benefits from this technique is backprojection, an image formation algorithm that can be used as part of a synthetic aperture radar (SAR) processing system. We present an implementation of backprojection for SAR on an HPRC system. Using simulated data taken at a variety of ranges, our implementation runs over 200 times faster than a similar software program, with an overall application speedup better than 50x. The backprojection application is easily parallelizable, achieving near-linear speedup when run on multiple nodes of a clustered HPRC system. The results presented can be applied to other systems and other algorithms with similar characteristics.
1. Introduction
In the continuing quest for computing architectures that are capable of solving more computationally complex problems, a new direction of study is high-performance reconfigurable computing (HPRC). HPRC can be defined as a marriage of traditional high-performance computing (HPC) techniques and reconfigurable computing (RC) devices.
HPC is a well-known set of architectural solutions for speeding up the computation of problems that can be divided neatly into pieces. Multiple general-purpose processors (GPPs) are linked together with high-speed networks and storage devices such that they can share data. Pieces of the problem are then distributed to the individual processors and computed, and the answer is assembled from the pieces. Commonly available HPC systems include Beowulf clusters and other supercomputers. Reconfigurable computing uses many of the same concepts as HPC, but at a finer grain. A special-purpose processor (SPP), often a field-programmable gate array (FPGA), is attached to a GPP and programmed to execute a useful function. Special-purpose hardware computes the answer to the problem quickly by exploiting hardware design techniques such as pipelining, the replication of small computation units, and high-bandwidth local memories.
Both of these computing architectures reduce computation time by exploiting the parallelism inherent in the application. They rely on the fact that multiple parts of the overall problem can be computed relatively independently of each other. Though HPC and RC act on different levels of parallelism, in general, applications with a high degree of parallelism are well-suited to these architectures.
The idea behind HPRC is to provide a computing architecture that takes advantage of both the coarse-grained parallelism exploited by clustered HPC systems and the fine-grained parallelism exploited by RC systems. In theory, more exploited parallelism means more speedup and faster computation times. In reality, factors such as communications bandwidth may prevent performance from improving as much as is desired.
In this paper, we examine one application that contains a very high degree of parallelism. The backprojection image formation algorithm for synthetic aperture radar (SAR) systems is "embarrassingly parallel", meaning that it can be broken down and parallelized on many different levels. For this reason, we chose to implement backprojection on an HPRC machine at the Air Force Research Laboratory in Rome, NY, USA, as part of an SAR processing system. We present an analysis of the algorithm and its inherent parallelism, and we describe the implementation process along with the design decisions that went into the solution.
Our contributions are as follows.
-
(i)
We implement the backprojection algorithm for SAR on an FPGA. Though backprojection has been implemented many times in the past (see Section 3), FPGA implementations of backprojection for SAR are not well represented in the literature.
-
(ii)
We further parallelize this implementation by developing an HPC application that produces large SAR images on a multinode HPRC system.
The rest of this paper is organized as follows. Section 2 provides some background information on the backprojection algorithm and the HPRC system on which we implemented it. In Section 3, we discuss related research. Section 4 describes the backprojection implementation and how it fits into the overall backprojection application. The performance data and results of our design experiments are analyzed in Section 5. Finally, Section 6 draws conclusions and suggests future directions for research.
Readers who are interested in more detail about this work are directed to the master thesis on which it is based [1].
2. Background
This section provides supporting information that is useful to understanding the application presented in Section 4. Section 2.1 describes backprojection and SAR, highlighting the mathematical function that we implemented in hardware. Section 2.2 presents details about the HPRC system that hosts our application.
2.1. Backprojection Algorithm
We briefly describe the backprojection algorithm in this section. Further details on the radar processing and signal processing aspects of this process can be found in [2, 3].
Backprojection is an image reconstruction algorithm that is used in a number of applications, including medical imaging (computed axial tomography, or (CAT)) and synthetic aperture radar (SAR). The implementation we describe is used in an SAR application. For both radar processing and medical imaging applications, backprojection provides a method for reconstructing an image from the data that are collected by the transceiver.
SAR data are essentially a series of time-indexed radar reflections observed by a single transceiver. At each step along the synthetic aperture, or flight path, a pulse is emitted from the source. This pulse reflects off elements in the scene to varying degrees, and is received by the transceiver. The observed response to a radar pulse is known as a "trace".
SAR data can be collected in one of two modes, "strip-map" or "spotlight". These modes describe the motion of the radar relative to the area being imaged. In the spotlight mode of SAR, the radar circles around the scene. Our application implements the strip-map mode of SAR, in which radar travels along a straight and level path.
Regardless of mode, given a known speed at which the radar pulse travels, the information from the series of time-indexed reflections can be used to identify points of high reflectivity in the target area. By processing multiple traces instead of just one, a larger radar aperture is synthesized and thus a higher-resolution image can be formed.
The backprojection image formation algorithm has two parts. First, the radar traces are filtered according to a linear time-invariant system. This filter accounts for the fact that the airplane on which the radar dish is situated does not fly in a perfectly level and perfectly straight path. Second, after filtering, the traces are "smeared" across an image plane along contours that are defined by the SAR mode; in our case, the flight path of the plane carrying the radar. Coherently, summing each of the projected images provides the final reconstructed version of the scene.
Backprojection is a highly effective method of processing SAR images. It is computationally complex, much like traditional Fourier-based image formation techniques. However, backprojection contains a high degree of parallelism, which makes it suitable for the implementation on reconfigurable devices.
The operation of backprojection takes the form of a mapping from projection data  to an image
to an image  . A single pixel of the image
. A single pixel of the image  corresponds to an area of ground containing some number of objects which reflect radar to a certain degree. Mathematically, this relationship is written as
corresponds to an area of ground containing some number of objects which reflect radar to a certain degree. Mathematically, this relationship is written as

where  is an indexing function indicating, at a given
is an indexing function indicating, at a given  , those
, those  that play a role in the value of the image at location
that play a role in the value of the image at location  . For the case of SAR imaging, the projection data
. For the case of SAR imaging, the projection data  take the form of the filtered radar traces described above. Thus, the variable
take the form of the filtered radar traces described above. Thus, the variable  corresponds to the slow-time location of the radar, and
corresponds to the slow-time location of the radar, and  is the fast-time index into that projection. Fast-time variables are related to the speed of radar propagation (i.e., the speed of light), while slow-time variables are related to the speed of the airplane carrying the radar. The indexing function
is the fast-time index into that projection. Fast-time variables are related to the speed of radar propagation (i.e., the speed of light), while slow-time variables are related to the speed of the airplane carrying the radar. The indexing function  takes the following form for SAR:
takes the following form for SAR:

where  is the speed of light,
is the speed of light,  the beamwidth of the radar, and
the beamwidth of the radar, and  equal to 1 for
equal to 1 for  and 0 otherwise.
and 0 otherwise.  and
and  describe the two-dimensional offset between the radar and the physical spot on the ground corresponding to a pixel, and can thus be used in a simple distance calculation as seen in the right-hand side of (2).
describe the two-dimensional offset between the radar and the physical spot on the ground corresponding to a pixel, and can thus be used in a simple distance calculation as seen in the right-hand side of (2).
In terms of implementation, we work with a discretized form of (1) in which the integral is approximated as a Riemann sum over a finite collection of projections  and is evaluated at the centers of image pixels
and is evaluated at the centers of image pixels  . Because the evaluation of the index function at these discrete points will generally not result in a value of
. Because the evaluation of the index function at these discrete points will generally not result in a value of  which is exactly at a sample location, interpolation could be performed to increase accuracy.
which is exactly at a sample location, interpolation could be performed to increase accuracy.
2.2. HPRC Architecture
This project aimed at exploiting the full range of resources available on the heterogeneous high-performance cluster (HHPC) at the Air Force Research Laboratory in Rome, NY, USA [4]. Built by HPTi [5], the HHPC features a Beowulf cluster of 48 heterogeneous computing nodes, where each node consists of a dual 2.2 GHz Xeon PC running Linux and an Annapolis Microsystems WildStar II FPGA board.
The WildStar II features two VirtexII FPGAs and connects to the host Xeon general-purpose processors (GPPs) via the PCI bus. Each FPGA has access to 6 MB of SRAM, divided into 6 banks of 1 MB each, and a single 64 MB SDRAM bank. The Annapolis API supports a master-slave paradigm for control and data transfer between the GPPs and the FPGAs. Applications for the FPGA can be designed either through traditional HDL-based design and synthesis tools, as we have done here, or by using Annapolis's CoreFire [6] module-based design suite.
The nodes of the HHPC are linked together in three ways. The PCs are directly connected via gigabit Ethernet as well as through Myrinet MPI cards. The WildStar II boards are also directly connected to each other through a low-voltage differential signaling (LVDS) I/O daughter card, which provides a systolic interface over which each FPGA board may talk to its nearest neighbor in a ring. Communication over Ethernet is supplied by the standard C library under Linux. Communication over Myrinet is achieved with an installation of the MPI message-passing standard, though MPI can also be directed to use Ethernet instead. Communicating through the LVDS interconnect involves writing communication modules for the FPGA manually. In this project, we relied on Myrinet to move data between nodes. This architecture represents perhaps the most direct method for adding reconfigurable resources to a supercomputing cluster. Each node architecture is similar to that of a single-node reconfigurable computing solution. Networking hardware which interfaces well to the Linux PCs is included to create the cluster network. The ability to communicate between FPGAs is included but remains difficult for the developer to employ. Other HPRC platforms, such as those developed by Cray and SRC, may employ different interconnection methods, programming methods, and communication paradigms.
3. Related Work
Backprojection itself is a well-studied algorithm. Most researchers have focused on implementing backprojection for computed tomography (CT) medical imaging applications; backprojection for synthetic aperture radar (SAR) on FPGAs is not well-represented in the literature.
The precursor to this work is that of Coric et al. [7] Backprojection for CT uses the "spotlight" mode of imaging, in which the sensing array is rotated around the target area. (Contrast this with the "strip-map" mode described in Section 2.1.) Other implementations of backprojection for CT on FPGAs have been published [8].
CT backprojection has also been implemented on several other computing devices, including GPUs [9] and the cell broadband engine [10]. Results are generally similar (within a factor of 2) to those achieved on FPGAs.
Of the implementations of backprojection for SAR, almost none has been designed for FPGAs. Soumekh et al. have published on implementations of SAR in general and backprojection in particular [11], as well as the Soumekh reference book on the subject [2], but they do not examine the use of FPGAs for computation. Some recent work on backprojection for SAR on parallel hardware has come from Halmstad University in Sweden [12, 13]; their publications lay important groundwork but have not been implemented except in software and/or simulation.
Backprojection is not the only application that has been mapped to HPRC platforms, though signal processing is traditionally a strength of RC and so large and complex signal processing applications like backprojection are common. With the emergence of HPRC, scientific applications are also seeing significant research effort. Among these are such applications as hyperspectral dimensionality reduction [14], molecular dynamics [15, 16], and cellular automata simulations [17].
Another direction of HPRC research has been the development of libraries of small kernels that are useful as building blocks for larger applications. The Vforce framework [18] allows for portable programming of RC systems using a library of kernels. Other developments include libraries of floating-point arithmetic units [19], work on FFTs [20], and linear algebra kernels such as BLAS [21, 22].
Several survey papers [23, 24] address the trends that can be found among the reported results. The transfer of data between GPP and FPGA can significantly impact performance. The ability to determine and control the memory access patterns of the FPGA and the on-board memories is critical. Finally, sacrificing the accuracy of the results in favor of using lighter-weight operations that can be more easily implemented on an FPGA can be an effective way of increasing performance.
4. Experimental Design
In this section, we describe an implementation of the backprojection image formation algorithm on a high-performance reconfigurable computer. Our implementation has been designed to provide high-speed image formation services and support output data distribution via a publish/subscribe [25] methodology. Section 4.1 describes the system on which our implementation runs. Section 4.2 explores the inherent parallelism in backprojection and describes the high-level design decisions that steered the implementation. Section 4.3 describes the portion of the implementation that runs in software, and Section 4.4 describes the hardware.
4.1. System Background
In Section 2.2, we described the HHPC system. In this section, we will explore more deeply the aspects of that system that are relevant to our experimental design.
4.1.1. HHPC Features
Several features of the Annapolis WildStar II FPGA boards are directly relevant to the design of our backprojection implementation. In particular, the host-to-FPGA interface, the on-board memory bandwidth, and the available features of the FPGA itself guided our design decisions.
Communication between the host GPP and the WildStar II board is over a PCI bus. The HHPC provides a PCI bus that runs at 66 MHz with 64-bit datawords. The WildStar II on-board PCI interface translates this into a 32-bit interface running at 133 MHz. By implementing the DMA data transfer mode to communicate between the GPP and the FPGA, the on-board PCI interface performs this translation invisibly and without significant loss of performance. A 133 MHz clock is also a good and achievable clock rate for FPGA hardware, so most of the hardware design can be run directly off the PCI interface clock. This simplifies the design since there are fewer clock domains (see Section 4.4.1).
The WildStar II board has six on-board SRAM memories (1 MB each) and one SDRAM memory (64 MB). It is beneficial to be able to read one datum and write one datum in the same clock cycle, so we prefer to use multiple SRAMs instead of the single larger SDRAM. The SRAMs run at 50 MHz and feature a 32-bit dataword (plus four parity bits), but they use a DDR interface. The Annapolis controller for the SRAM translates this into a 50 MHz 72-bit interface. Both features are separately important: we will need to cross from the 50 MHz memory clock domain to the 133 MHz PCI clock domain, and we will need to choose the size of our data such that they can be packed into a 72-bit memory word (see Section 4.2.4).
Finally, the Virtex2 6000 FPGA on the Wildstar II has some useful features that we use to our advantage. A large amount of on-chip memory is available in the form of BlockRAMs, which are configurable in width and depth but can hold at most 2 KB of data each. One hundred forty four of these dual-ported memories are available, each of which can be accessed independently. This makes BlockRAMs a good candidate for storing and accessing input projection data (see Sections 4.2.4 and 4.4.3.) BlockRAMs can also be configured as FIFOs, and due to their dual-ported nature, can be used to cross clock domains.
4.1.2. Swathbuckler Project
This project was designed to fit in as part of the Swathbuckler project [26–28], an implementation of synthetic aperture radar created by a joint program between the American, British, Canadian, and Australian defense research project agencies. It encompasses the entire SAR process including the aircraft and radar dish, signal capture and analog-to-digital conversion, filtering, and image formation hardware and software.
Our problem as posed was to increase the processing capabilities of the HHPC by increasing the performance of the portions of the application seen on the right-hand side of Figure 1. Given that a significant amount of work had gone into tuning the performance of the software implementation of the filtering process [26], it remained for us to improve the speed at which images could be formed. According to the project specification, the input data are streamed into the microprocessor main memory. In order to perform image formation on the FPGA, it is then necessary to copy data from the host to the FPGA. Likewise, the output image must be copied from the FPGA memory to the host memory so that it can be made accessible to the publish/subscribe software. These data transfer times are included in our performance measurements (see Section 5).
Block diagram of Swathbuckler system. (Adapted from [26].)
4.2. Algorithm Analysis
In this section, we dissect the backprojection algorithm with an eye toward implementing it on an HPRC machine. There are many factors that need to be taken into account when designing an HPRC application. First and foremost, an application that does not have a high degree of parallelism is generally not a good candidate. Given a suitable application, we then decide how to divide the problem along the available levels of parallelism in order to determine what part of the application will be executed on each available processor. This includes GPP/FPGA assignment as well as dividing the problem across the multiple nodes of the cluster. For the portions of the application run on the FPGAs, data arrays must be distributed among the accessible memories. Next, we look at some factors to improve the performance of the hardware implementation, namely, data formats and computation strength reduction. We conclude by examining the parameters of the data collection process that affect the computation.
4.2.1. Parallelism Analysis
In any reconfigurable application design, performance gains due to implementation in hardware inevitably come from the ability of reconfigurable hardware (and, indeed, hardware in general) to perform multiple operations at once. Extracting the parallelism in an application is thus critical to a high-performance implementation.
Equation (1) shows the backprojection operation in terms of projection data  and an output image
and an output image  . That equation may be interpreted to say that for a particular pixel
. That equation may be interpreted to say that for a particular pixel  , the final value can be found from a summation of contributions from the set of all projections
, the final value can be found from a summation of contributions from the set of all projections  whose corresponding radar pulse covered that ground location. The value of
whose corresponding radar pulse covered that ground location. The value of  for a given
for a given  is determined by the mapping function
is determined by the mapping function  according to (2). There is a large degree of parallelism inherent in this interpretation.
according to (2). There is a large degree of parallelism inherent in this interpretation.
-
(1)
The contribution from projection
 to pixel
to pixel 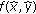 is not dependent on the contributions from all other projections
is not dependent on the contributions from all other projections  to that same pixel
to that same pixel  .
. -
(2)
The contribution from projection
 to pixel
to pixel 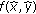 is not dependent on the contribution from
is not dependent on the contribution from  to all other pixels
to all other pixels 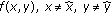 .
. -
(3)
The final value of a pixel is not dependent on the value of any other pixel in the target image.
It can be said, therefore, that backprojection is an "embarrassingly parallel" application, which is to say that it lacks any data dependencies. Without data dependencies, the opportunity for parallelism is vast and it is simply a matter of choosing the dimensions along which to divide the computation that best matches the system on which the algorithm will be implemented.
4.2.2. Dividing the Problem
There are two ways in which parallel applications are generally divided across the nodes of a cluster.
-
(1)
Split the data. In this case, each node performs the same computation as every other node, but on a subset of data. There may be several different ways that the data can be divided.
-
(2)
Split the computation. In this case, each node performs a portion of the computation on the entire dataset. Intermediate sets of data flow from one node to the next. This method is also known as task-parallel or systolic computing.
While certain supercomputer networks may make the task-parallel model attractive, our work with the HHPC indicates that its architecture is more suited to the data-parallel mode. Since internode communication is accomplished over a many-to-many network (Ethernet or Myrinet), passing data from one node to the next as implied by the task-parallel model will potentially hurt performance. A task-parallel design also implies that a new FPGA design must be created for each FPGA node in the system, greatly increasing design and verification time. Finally, the number of tasks available in this application is relatively small and would not occupy the number of nodes that are available to us.
Given that we will create a data-parallel design, there are several axes along which we considered splitting the data. One method involves dividing the input projection data  among the nodes along the
among the nodes along the  dimension. Each node would hold a portion of the projections
dimension. Each node would hold a portion of the projections  and calculate that portion contribution to the final image. However, this implies that each node must hold a copy of the entire target image in memory, and furthermore, that all of the partial target images would need to be added together after processing before the final image could be created. This extra processing step would also require a large amount of data to pass between nodes. In addition, the size of the final image would be limited to that which would fit on a single FPGA board.
and calculate that portion contribution to the final image. However, this implies that each node must hold a copy of the entire target image in memory, and furthermore, that all of the partial target images would need to be added together after processing before the final image could be created. This extra processing step would also require a large amount of data to pass between nodes. In addition, the size of the final image would be limited to that which would fit on a single FPGA board.
Rather than dividing the input data, the preferred method divides the output image  into pieces along the range (
into pieces along the range ( ) axis (see Figure 2). In theory, this requires that every projection be sent to each node; however, since only a portion of each projection will affect the slice of the final image being computed on a single node, only that portion must be sent to that node. Thus, the amount of input data being sent to each node can be reduced to
) axis (see Figure 2). In theory, this requires that every projection be sent to each node; however, since only a portion of each projection will affect the slice of the final image being computed on a single node, only that portion must be sent to that node. Thus, the amount of input data being sent to each node can be reduced to  . We refer to the portion of the final target image being computed on a single node,
. We refer to the portion of the final target image being computed on a single node,  , as a "subimage".
, as a "subimage".
Figure 2 shows that  is slightly beyond the time index that corresponds to
is slightly beyond the time index that corresponds to  . This is due to the width of the cone-shaped radar beam. The dotted line in the figure shows a single radar pulse taken at slow-time index
. This is due to the width of the cone-shaped radar beam. The dotted line in the figure shows a single radar pulse taken at slow-time index  . The minimum distance to any part of the subimage is at the point
. The minimum distance to any part of the subimage is at the point  , which corresponds to fast-time index
, which corresponds to fast-time index  in the projection data. The maximum distance to any part of the subimage, however, is along the outer edge of the cone to the point
in the projection data. The maximum distance to any part of the subimage, however, is along the outer edge of the cone to the point  where
where  is a factor calculated from the beamwidth angle of the radar and
is a factor calculated from the beamwidth angle of the radar and  . Thus, the fast-time index
. Thus, the fast-time index  is calculated relative to
is calculated relative to  and
and  instead of simply
instead of simply  . This also implies that the
. This also implies that the  range for two adjacent nodes will overlap somewhat, or (equivalently) that some projection data will be sent to more than one node.
range for two adjacent nodes will overlap somewhat, or (equivalently) that some projection data will be sent to more than one node.
Since the final value of a pixel does not depend on the values of the pixels surrounding it, each FPGA needs hold only the subimage that it is responsible for computing. That portion is not affected by the results on any other FPGA, which means that the postprocessing accumulation stage can be avoided. If a larger target image is desired, subimages can be "stitched" together simply by concatenation.
In contrast to the method where input data are divided along the  dimension, the size of the final target image is not restricted by the amount of memory on a single node, and furthermore, larger images can be processed by adding nodes to the cluster. This is commonly referred to as coarse-grained parallelism, since the problem has been divided into large-scale independent units. Coarse-grained parallelism is directly related to the performance gains that are achieved by adapting the application from a single-node computer to a multinode cluster.
dimension, the size of the final target image is not restricted by the amount of memory on a single node, and furthermore, larger images can be processed by adding nodes to the cluster. This is commonly referred to as coarse-grained parallelism, since the problem has been divided into large-scale independent units. Coarse-grained parallelism is directly related to the performance gains that are achieved by adapting the application from a single-node computer to a multinode cluster.
4.2.3. Memory Allocation
The memory devices used to store the input and output data on the FPGA board may now be determined. We need to store two large arrays of information: the target image  and the input projection data
and the input projection data  . On the Wildstar II board, there are three options: an on-board DRAM, six on-board SRAMs, and a variable number of BlockRAMs which reside inside the FPGA and can be instantiated as needed. The on-board DRAM has the highest capacity (64 MB) but is the most difficult to use and only has one read/write port. BlockRAMs are the most flexible (two read/write ports and a flexible geometry) and simple to use, but have a small (2 KB) capacity.
. On the Wildstar II board, there are three options: an on-board DRAM, six on-board SRAMs, and a variable number of BlockRAMs which reside inside the FPGA and can be instantiated as needed. The on-board DRAM has the highest capacity (64 MB) but is the most difficult to use and only has one read/write port. BlockRAMs are the most flexible (two read/write ports and a flexible geometry) and simple to use, but have a small (2 KB) capacity.
For the target image, we would like to be able to both read and write one target pixel per cycle. It is also important that the size of the target image stored on one node be as large as possible, so memories with larger capacity are better. Thus, we will use multiple on-board SRAMs to store the target image. By implementing a two-memory storage system, we can provide two logical ports into the target image array. During any given processing step, one SRAM acts as the source for target pixels, and the other acts as the destination for the newly computed pixel values. When the next set of projections is sent to the FPGA, the roles of the two SRAMs are reversed.
Owing to the 1 MB size of the SRAMs in which we store the target image data, we are able to save  pixels. We choose to arrange this into a target image that is 1024 pixels in the azimuth dimension and 512 in the range dimension. Using power-of-two dimensions allows us to maximize our use of the SRAM, and keeping the range dimension small allows us to reduce the amount of projection data that must be transferred.
pixels. We choose to arrange this into a target image that is 1024 pixels in the azimuth dimension and 512 in the range dimension. Using power-of-two dimensions allows us to maximize our use of the SRAM, and keeping the range dimension small allows us to reduce the amount of projection data that must be transferred.
For the projection data, we would like to have many small memories that can each feed one of the projection adder units. BlockRAMs allow us to instantiate multiple small memories in which to hold the projection data; each memory has two available ports, meaning that two adders can be supported in parallel. Each adder reads from one SRAM and writes to another; since we can support two adders, we could potentially use four SRAMs.
4.2.4. Data Formats
Backprojection is generally accomplished in software using a complex (i.e., real and imaginary parts) floating-point format. However, since the result of this application is an image which requires only values from 0 to 255 (i.e., 8-bit integers), the loss of precision inherent in transforming the data to a fixed-point/integer format is negligible. In addition, using an integer data format allows for much simpler functional units.
Given an integer data format, it remains to determine how wide the various datawords should be. We base our decision on the word width of the memories. The SRAM interface provides 72 bits of data per cycle, comprised of two physical 32-bit datawords plus four bits of parity each. The BlockRAMs are configurable, but generally can provide power-of-two sized datawords.
Since backprojection is in essence an accumulation operation, it makes sense for the output data (target image pixels) to be wider than the input data (projection samples). This reduces the likelihood of overflow error in the accumulation. We, therefore, use 36-bit complex integers (18-bit real and 18-bit imaginary) for the target image, and 32-bit complex integers for the projection data.
After backprojection, a complex magnitude operator is needed to reduce the 36-bit complex integers to a single 18-bit real integer. This operator is implemented in hardware, but the process of scaling data from 18-bit integer to 8-bit image is left to the software running on the GPP.
4.2.5. Computation Analysis
The computation to be performed on each node consists of three parts. The summation from (1) and the distance calculation from (2) represent the backprojection work to be done. The complex magnitude operation is similar to the distance calculation.
While adders are simple to replicate in large numbers, the hardware required to perform multiplication and square root is more costly. If we were using floating-point data formats, the number of functional units that could be instantiated would be very small, reducing the parallelism that we can exploit. With integer data types, however, these units are relatively small, fast, and easily pipelined. This allows us to maintain a high clock rate and one-result-per-cycle throughput.
4.2.6. Data Collection Parameters
The conditions under which the projection data are collected affect certain aspects of the backprojection computation. In particular, the spacing between samples in the  array and the spacing between pixels in the
array and the spacing between pixels in the  array imply constant factors that must be accounted for during the distance-to-time index calculation (see Section 4.4.3).
array imply constant factors that must be accounted for during the distance-to-time index calculation (see Section 4.4.3).
For the input data,  indicates the distance (in meters) between samples in the azimuth dimension. This is equivalent to the distance that the plane travels between each outgoing pulse of the radar. Often, due to imperfect flight paths, this value is not regular. The data filtering that occurs prior to backprojection image formation is responsible for correcting for inaccuracies due to the actual flight path, so that a regular spacing can be assumed.
indicates the distance (in meters) between samples in the azimuth dimension. This is equivalent to the distance that the plane travels between each outgoing pulse of the radar. Often, due to imperfect flight paths, this value is not regular. The data filtering that occurs prior to backprojection image formation is responsible for correcting for inaccuracies due to the actual flight path, so that a regular spacing can be assumed.
As the reflected radar data are observed by the radar receiver, they are sampled at a particular frequency  . That frequency translates to a range distance
. That frequency translates to a range distance  between samples equal to
between samples equal to  , where
, where  is the speed of light. The additional factor of
is the speed of light. The additional factor of  accounts for the fact that the radar pulse travels the intervening distance, is reflected, and travels the same distance back. Owing to the fact that the airplane is not flying at ground level, there is an additional angle of elevation that is included to determine a more accurate value for
accounts for the fact that the radar pulse travels the intervening distance, is reflected, and travels the same distance back. Owing to the fact that the airplane is not flying at ground level, there is an additional angle of elevation that is included to determine a more accurate value for  .
.
For the target image (output data),  and
and  simply correspond to the real distance between pixels in the range and azimuth dimensions, accordingly. In general,
simply correspond to the real distance between pixels in the range and azimuth dimensions, accordingly. In general,  and
and  are not necessarily related to
are not necessarily related to  and
and  and can be chosen at will. In practice, setting
and can be chosen at will. In practice, setting  makes the algorithm computation more regular (and thus more easily parallelizable). Likewise, setting
makes the algorithm computation more regular (and thus more easily parallelizable). Likewise, setting  reduces the need for interpolation between samples in the
reduces the need for interpolation between samples in the  dimension since most samples will line up with pixels in the range dimension. Finally, setting
dimension since most samples will line up with pixels in the range dimension. Finally, setting  provides for square pixels and an easier-to-read aspect ratio in the output image.
provides for square pixels and an easier-to-read aspect ratio in the output image.
The final important parameter is the minimum range from the radar to the target image, known as  . This is related to the
. This is related to the  parameter, and is used by the software to determine what portion of the projection data is applicable to a particular node.
parameter, and is used by the software to determine what portion of the projection data is applicable to a particular node.
4.3. Software Design
We now describe the HPRC implementation of backprojection. As with most FPGA-based applications, the work that makes up the application is divided between the host GPP and the FPGA. In this section, we will discuss the work done on the GPP; in Section 4.4, we continue with the hardware implemented on the FPGA.
The main executable running on the GPP begins by using the MPI library to spawn processes on several of the HHPC nodes. Once all MPI jobs have started, the host code configures the FPGA with the current values of the flight parameters from Section 4.2.6. In particular, the values of  and
and  (the minimum range) are sent to the FPGA. However, in order to avoid the use of fractional numbers, all of these parameters are normalized such that
(the minimum range) are sent to the FPGA. However, in order to avoid the use of fractional numbers, all of these parameters are normalized such that  . This allows the hardware computation to be in terms of fast-time indices in the
. This allows the hardware computation to be in terms of fast-time indices in the  domain instead of ground distances.
domain instead of ground distances.
Next, the radar data is read. In the Swathbuckler system, this input data would be streamed directly into memory and no separate "read" step would be required. Since we are not able to integrate directly with Swathbuckler, our host code reads the data from a file on the shared disk. These data are translated from complex floating-point format to integers. The host code also determines the appropriate range of  that is relevant to the subimage being calculated by this node (see Section 4.2.2).
that is relevant to the subimage being calculated by this node (see Section 4.2.2).
The host code then loops over the  domain of the projection data. A chunk of the data is sent to the FPGA and processed. The host code waits until the FPGA signals processing is complete, and then transmits the next chunk of data. When all projection data have been processed, the host code requests that the final target image be sent from the FPGA. The pixels of the target image are scaled, rearranged into an image buffer, and an image file is optionally produced using a library call to the GTK+ library [29].
domain of the projection data. A chunk of the data is sent to the FPGA and processed. The host code waits until the FPGA signals processing is complete, and then transmits the next chunk of data. When all projection data have been processed, the host code requests that the final target image be sent from the FPGA. The pixels of the target image are scaled, rearranged into an image buffer, and an image file is optionally produced using a library call to the GTK+ library [29].
After processing, the target subimages are simply held in the GPP memory. In the Swathbuckler system, subimages are distributed to consumers via a publish/subscribe mechanism, so there is no need to assemble all the subimages into a larger image.
4.3.1. Configuration Parameters
Our backprojection implementation can be configured using several compile-time parameters in both the host code and the VHDL code that describes the hardware. In software, the values of  and
and  are set in the header file and compiled in. The value of
are set in the header file and compiled in. The value of  is specific to a dataset, so it is read from the file that contains the projection data.
is specific to a dataset, so it is read from the file that contains the projection data.
It is also possible to set the dimensions of the subimage ( by default), though the hardware would require significant changes to support this.
by default), though the hardware would require significant changes to support this.
The hardware VHDL code allows two parameters to be set at compile time (see Section 4.4.3).  is the number of projection adders in the design, and
is the number of projection adders in the design, and  is the size of the projection memories (
is the size of the projection memories ( words). Once compiled, the value of these parameters can be read from the FPGA by the host code.
words). Once compiled, the value of these parameters can be read from the FPGA by the host code.
4.4. FPGA Design
The hardware that is instantiated on the FPGA boards runs the backprojection algorithm and computes the values of the pixels in the output image. A block diagram of the design is shown in Figure 3. References to blocks in this figure are printed in  .
.
4.4.1. Clock Domains
In general, using multiple clock domains in a design adds complexity and makes verification significantly more difficult. However, the design of the Annapolis Wildstar II board provides for one fixed-rate clock on the PCI interface, and a separate fixed-rate clock on the SRAM memories. This is a common attribute of FPGA-based systems.
To simplify the problem, we run the bulk of our design at the PCI clock rate (133 MHz). Since Annapolis VHDL modules refer to the PCI interface as the "LAD bus", we call this the L-clock domain. Every block in Figure 3, with the exception of the SRAMs themselves and their associated  , is run from the L-clock.
, is run from the L-clock.
The SRAMs are run from the memory clock, or M-clock, which is constrained to run at 50 MHz. Between the  and the
and the  , there is some interface logic and an FIFO. This is not shown in Figure 3, but exists to cross the M-clock/L-clock domain boundary.
, there is some interface logic and an FIFO. This is not shown in Figure 3, but exists to cross the M-clock/L-clock domain boundary.
BlockRAM-based FIFOs, available as modules in the Xilinx CORE Generator [30] library, are used to cross clock domains. Since each of the ports on the dual-ported BlockRAMs is individually clocked, the read and write can happen in different clock domains. Control signals are automatically synchronized to the appropriate clock, that is, the "full" signal is synchronized to the write clock and the "empty" signal to the read clock. Using FIFOs whenever clock domains must be crossed provides a simple and effective solution.
4.4.2. Control Registers and DMA Input
The Annapolis API, like many FPGA control APIs, allows for communication between the host PC and the FPGA with two methods: "programmed" or memory-mapped I/O (PIO), which is best for reading and writing one or two words of data at a time; direct memory access (DMA), which is best for transferring large blocks of data.
The host software uses PIO to set control registers on the FPGA. Projection data is placed in a specially allocated memory buffer, and then transmitted to the FPGA via DMA. On the FPGA, the  receives the data and arranges it in the BlockRAMs inside the
receives the data and arranges it in the BlockRAMs inside the  .
.
4.4.3. Datapath
The main datapath of the backprojection hardware is shown in Figure 4. It consists of five parts: the  SRAMs that hold the target image, the
SRAMs that hold the target image, the  -
- -
- (DIC), the
(DIC), the 
 , the
, the  to perform the accumulation operation, and the
to perform the accumulation operation, and the  that drive all of the memories. These devices all operate in a synchronized fashion, though there are FIFOs in several places to temporally decouple the producers and consumers of data, as indicated in Figure 4 with segmented rectangles.
that drive all of the memories. These devices all operate in a synchronized fashion, though there are FIFOs in several places to temporally decouple the producers and consumers of data, as indicated in Figure 4 with segmented rectangles.
Address Generators
There are three data arrays that must be managed in this design: the input target data, the output target data, and the projection data. The pixel indices for the two target data arrays ( in Figure 4) are managed directly by separate address generators. The address generator for the
in Figure 4) are managed directly by separate address generators. The address generator for the  also produces pixel indices; the DIC converts the pixel index into a fast-time index that is used to address the BlockRAMs.
also produces pixel indices; the DIC converts the pixel index into a fast-time index that is used to address the BlockRAMs.
Because a single read/write operation to the SRAMs produces/consumes two pixel values, the address generators for the SRAMs run for half as many cycles as the address generator for the BlockRAMs. However, address generators run in the clock domain relevant to the memory that they are addressing, so  SRAM addresses take slightly longer to generate at 50 MHz than
SRAM addresses take slightly longer to generate at 50 MHz than  BlockRAM addresses at 133 MHz.
BlockRAM addresses at 133 MHz.
Because of the use of FIFOs between the memories and the adders, the address generators for  and the
and the  can run freely. FIFO control signals ensure that an address generator is paused in time to prevent it from overflowing the FIFO. The address generator for
can run freely. FIFO control signals ensure that an address generator is paused in time to prevent it from overflowing the FIFO. The address generator for  is incremented whenever data are available from the output FIFO.
is incremented whenever data are available from the output FIFO.
Distance-to-Time Index Calculator
The  -
- -
- (DIC) implements (2), which is comprised of two parts. At first glance, each of these parts involves computation that requires large amount of hardware and/or time to calculate. However, a few simplifying assumptions make this problem easier and reduce the amount of needed hardware.
(DIC) implements (2), which is comprised of two parts. At first glance, each of these parts involves computation that requires large amount of hardware and/or time to calculate. However, a few simplifying assumptions make this problem easier and reduce the amount of needed hardware.
Rather than implementing a tangent function in hardware, we rely on the fact that the beamwidth  of the radar is a constant. The host code performs the
of the radar is a constant. The host code performs the  function and sends the result to the FPGA, which is then used to calculate
function and sends the result to the FPGA, which is then used to calculate  . This value is used both on a coarse-grained level to narrow the range of pixels which are examined for each processing step, and on a fine-grained level to determine whether or not a particular pixel is affected by the current projection (see Figure 2).
. This value is used both on a coarse-grained level to narrow the range of pixels which are examined for each processing step, and on a fine-grained level to determine whether or not a particular pixel is affected by the current projection (see Figure 2).
The right-hand side of (2) is a distance function ( ) and a division. The square root function is executed using an iterative shift-and-subtract algorithm. In hardware, this algorithm is implemented with a pipeline of subtractors. Two multiplication units handle the
) and a division. The square root function is executed using an iterative shift-and-subtract algorithm. In hardware, this algorithm is implemented with a pipeline of subtractors. Two multiplication units handle the  and
and  functions. Some additional adders and subtractors are necessary to properly align the input data to the output data according to the data collection parameters discussed in Section 4.2.6. We used pipelined multipliers and division units from the Xilinx CORE Generator library; adders and subtractors are described with VHDL arithmetic operators, allowing the synthesis tools to generate the appropriate hardware.
functions. Some additional adders and subtractors are necessary to properly align the input data to the output data according to the data collection parameters discussed in Section 4.2.6. We used pipelined multipliers and division units from the Xilinx CORE Generator library; adders and subtractors are described with VHDL arithmetic operators, allowing the synthesis tools to generate the appropriate hardware.
The distance function and computation of  occur in parallel. If the
occur in parallel. If the  function determines that the pixel is outside the affected range, the adder input is forced to zero.
function determines that the pixel is outside the affected range, the adder input is forced to zero.
Projection Data Blockrams
The output of the DIC is a fast-time index into the  array. Each
array. Each  BlockRAM holds the data for a particular value of
BlockRAM holds the data for a particular value of  . The fast-time index
. The fast-time index  is applied to retrieve a single value of
is applied to retrieve a single value of  that corresponds to the pixel that was input by the address generator. This value is stored in an FIFO, to be synchronized with the output of the
that corresponds to the pixel that was input by the address generator. This value is stored in an FIFO, to be synchronized with the output of the  FIFO.
FIFO.
 memories are configured to hold 2 k datawords by default, which should be sufficient for a 1 k range pixel image. This number is a compile-time parameter in the VHDL source and can be changed. The resource constraint is the number of available BlockRAMs.
memories are configured to hold 2 k datawords by default, which should be sufficient for a 1 k range pixel image. This number is a compile-time parameter in the VHDL source and can be changed. The resource constraint is the number of available BlockRAMs.
Projection Adder
As the FIFOs from the  memories and the
memories and the  are filled, the
are filled, the  reads datawords from both FIFOs, adds them together, and passes them to the next stage in the pipeline (see Figure 4).
reads datawords from both FIFOs, adds them together, and passes them to the next stage in the pipeline (see Figure 4).
The design is configured with eight adder stages, meaning eight projections can be processed in one step. This number is a compile-time parameter in the VHDL source and can be changed. The resource constraint is a combination of the number of available BlockRAMs (because the  BlockRAMs and FIFO are duplicated) and the amount of available logic (to implement the DIC).
BlockRAMs and FIFO are duplicated) and the amount of available logic (to implement the DIC).
The number of adder stages implemented directly impacts the performance of our application. By computing the contribution of multiple projections in parallel, we exploit the fine-grained parallelism inherent in the backprojection algorithm. Fine-grained parallelism is directly related to the performance gains achieved by implementing the application in hardware, where many small execution units can be implemented that all run at the same time on different pieces of data.
4.4.4. Complex Magnitude and DMA Output
When all projections have been processed, the final target image data reside in one of the  SRAMs. The host code then requests that the image data be transferred via DMA to the host memory. This process occurs in three steps.
SRAMs. The host code then requests that the image data be transferred via DMA to the host memory. This process occurs in three steps.
First, an  reads the data out of the SRAM in the correct order. Second, the data are converted from complex to real. The
reads the data out of the SRAM in the correct order. Second, the data are converted from complex to real. The  operator performs this function with a distance calculation (
operator performs this function with a distance calculation ( ). We instantiate another series of multipliers, adders, and subtractors (for the integer square root) to perform this operation. Third, the real-valued pixels are passed to the
). We instantiate another series of multipliers, adders, and subtractors (for the integer square root) to perform this operation. Third, the real-valued pixels are passed to the  , where they are sent from the FPGA to the host memory.
, where they are sent from the FPGA to the host memory.
5. Experimental Results
After completing the design, we conducted a series of experiments to determine the performance and accuracy of the hardware. When run on a single node, a detailed profile of the execution time of both the software and hardware programs can be determined, and the effects of reconfigurable hardware design techniques can be studied. Running the same program on multiple nodes shows how well the application scales take advantage of the processing power available on HPC clusters. In this section, we describe the experiments and analyze the collected results.
5.1. Experimental Setup
Our experiments consist of running programs on the HHPC and measuring the run time of individual components as well as the overall execution time. There are two programs: one which forms images by running backprojection on the GPP (the "software" program), and one which runs it in hardware on an FPGA (the "hardware" program).
We are concerned with two factors: speed of execution and accuracy of solution. We will consider not only the execution time of the backprojection operation by itself, but also the execution time of the entire program including peripheral operations such as memory management and data scaling. In addition, we examine the full application run time.
In terms of accuracy, the software program computes its results in floating point while the hardware uses integer arithmetic. We will examine the differences between the images produced by these two programs in order to establish the error introduced by the data format conversion.
The ability of our programs to scale across multiple nodes is an additional performance metric. We measure the effectiveness of exploiting coarse-grained parallelism by comparing the relative performance of both the software program and the hardware implementation when run on one node and when run on many nodes.
5.1.1. Software Design
All experiments were conducted on the HHPC system as described in Section 2.2. Nodes on the HHPC run the Linux operating system, RedHat release 7.3, using kernel version 2.4.20.
Both the software program and the calling framework for the hardware implementation are written in C and produce an executable that is started from the Linux shell. The software program executes entirely on the GPP: memory buffers are established, projection data are read from disk, the backprojection algorithm is run, and output data are transformed from complex to real. The final step involves rearranging the output data and scaling it, then writing a PNG image to disk.
The hardware program begins by establishing memory buffers and initializing the FPGA. Projection data are read from disk into the GPP memory. Those data are then transferred to the FPGA, where the backprojection algorithm is run in hardware. Output data are transformed from complex to real on the FPGA, then transferred to the GPP memory. The GPP then executes the same rearrangement and scaling step as the software program.
To control the FPGA, the hardware program uses an API that is provided by Annapolis to interface to the WildStar II boards. The FPGA hardware was written in VHDL and synthesized using version 8.9 of Synplify Pro. Hardware place and route used the Xilinx ISE 9.1i suite of CAD tools.
The final step of both programs, where the target data are written as a PNG image to disk by the GPP, uses the GTK+ [29] library version 2.0.2. For the multinode experiments, version 1.2.1.7b of the MPICH [31] implementation of MPI is used to handle internode startup, communication, and synchronization.
The timing data presented in this section were collected using timing routines that were inserted into the C code. These routines use Linux system calls to display timing information. The performance of the timing routines was determined by running them several times in succession with no code in between. The overhead of the performance routines was shown to be less than 100 microseconds, so timing data are presented as accurate to the millisecond. Unless noted otherwise, applications were run five times and an average (arithmetic mean) was taken to arrive at the presented data.
We determine accuracy both qualitatively (i.e., by examining the images with the human eye) and quantitatively by computing the difference in pixel values between the two images.
5.1.2. Test Data
Four sets of data were used to test our programs. The datasets were produced using a MATLAB simulation of SAR taken from the Soumekh book [2]. This MATLAB script allows the parameters of the data collection process to be configured (see Section 4.2.6). When run, it generates the projection data that would be captured by an SAR system imaging that area. A separate C program takes the MATLAB output and converts it to an optimized file that can be read by the backprojection programs.
Each dataset contains four point source (i.e.,  pixel in size) targets that are distributed randomly through the imaged area. The imaged area for each set is of a similar size, but situated at a different distance from the radar. Targets are also assigned a random reflectivity value that indicates how strongly they reflect radar signals.
pixel in size) targets that are distributed randomly through the imaged area. The imaged area for each set is of a similar size, but situated at a different distance from the radar. Targets are also assigned a random reflectivity value that indicates how strongly they reflect radar signals.
5.2. Results and Analysis
In general, owing to the high degree of parallelism inherent in the backprojection algorithm, we expect a considerable performance benefit from implementation in hardware even on a single node. For the multinode program, the lack of need to transfer data between the nodes implies that the performance should scale in a linear relation to the number of nodes.
5.2.1. Single Node Performance
The first experiment involves running backprojection on a single node. This allows us to examine the performance improvement due to fine-grained parallelism, that is, the speedup that can be gained by implementing the algorithm in hardware. For this experiment, we ran the hardware and software programs on all four of the datasets. Table 1 shows the timing breakdown of dataset no. 4; Table 2 shows the overall results for all four datasets. Note that dataset no. 1 is closest to the radar, and dataset no. 4 is furthest away.
In Table 1, Software and Hardware refer to the run time of a particular component; Ratio is the ratio of software time to hardware time, showing the speedup or slowdown of the hardware program. Backprojection is the running of the core algorithm. Complex Magnitude transforms the data from complex to real integers. Finally, Form Image scales the data to the range [0:255] and creates the memory buffer that is used to create the PNG image.
There are a number of significant observations that can be made from the data in Table 1. Most importantly, the process of running the backprojection algorithm is greatly accelerated in hardware, running over 200x faster than our software implementation. It is important to emphasize that this includes the time required to transfer projection data from the host to the FPGA, which is not required by the software program. Many of the applications discussed in Section 3 exhibit only modest performance gains due to the considerable amount of time spent transferring data. Here, the vast degree of fine-grained parallelism in the backprojection algorithm that can be exploited by FPGA hardware allows us to achieve excellent performance compared to a serial software implementation.
The complex magnitude operator also runs about 5x faster in hardware. In this case, the transfer of the output data from the FPGA to the host is overlapped with the computation of the complex magnitude. This commonly used technique allows the data transfer time to be "hidden", preventing it from affecting overall performance.
However, the process of converting the backprojection output into an image buffer that can be converted to a PNG image (Form Image) runs faster when executed as part of the software program. This step is performed in software regardless of where the backprojection algorithm was executed. The difference in run time can be attributed to memory caching. When backprojection occurs in software, the result data lie in the processor cache. When backprojection occurs in hardware, the result data are copied via DMA into the processor main memory, and must be loaded into the cache before the Form Image step can begin.
We do not report the time required to initialize either the hardware or software program, since in the Swathbuckler system it is expected that initialization can be completed before the input data become available.
Table 2 shows the single-node performance of both programs on all four datasets. Note that the reported run times are only the times required by the backprojection operation. Thus, column four, BP Speedup, shows the factor of speedup (software:hardware ratio) for only the backprojection operation. Column five, App Speedup, shows the factor of speedup for the complete application including all of the steps shown in Table 1.
These results show that the computation time of the backprojection algorithm is data dependent. This is directly related to the minimum range of the projection data. According to Figure 2, as the subimage gets further away from the radar, the width of the radar beam is larger. This is reflected in the increased limits of the  term of (2), which are a function of the tangent of the beamwidth
term of (2), which are a function of the tangent of the beamwidth  and the range. A larger range implies more pixels are impacted by each projection, resulting in an increase in processing time. The hardware and software programs scale at approximately the same rate, which is expected since they are processing the same amount of additional data at longer ranges.
and the range. A larger range implies more pixels are impacted by each projection, resulting in an increase in processing time. The hardware and software programs scale at approximately the same rate, which is expected since they are processing the same amount of additional data at longer ranges.
More notable is the increase in application speedup; this can be explained by considering that the remainder of the application is not data dependent and stays relatively constant as the minimum range varies. Therefore, as the range increases and the amount of data to process increases, the backprojection operation takes up a larger percentage of the run time of the entire application. For software, this increase in proportion is negligible (99.5% to 99.8%), but for the hardware, it is quite large (12.6% to 25.0%). As the backprojection operator takes up more of the overall run time, the relative gains from implementing it in hardware become larger, resulting in the increasing speedup numbers seen in the table.
5.2.2. Single Node Accuracy
Qualitatively, the hardware images look very similar, with the hardware images perhaps slightly darker near the point source target. This is due to the quantization imposed by using integer data types. As discussed in Section 5.2.1, a longer range implies a wider radar beam. The  function from (2) determines how wide the beam is at a given range. When computed in fixed point for the hardware program,
function from (2) determines how wide the beam is at a given range. When computed in fixed point for the hardware program,  returns slightly different values than when the software program computes it in floating point. Thus, there is a slight smearing or blurring of the point source. Recall that dataset no. 4 has a longer range than the other datasets; appropriately, the smearing is most notable in that dataset.
returns slightly different values than when the software program computes it in floating point. Thus, there is a slight smearing or blurring of the point source. Recall that dataset no. 4 has a longer range than the other datasets; appropriately, the smearing is most notable in that dataset.
Quantitatively, the two images can be compared pixel-by-pixel to determine the differences. For each dataset, Table 3 presents error in terms of the differences between the image produced by the software program and the image produced by the hardware program.
The second column shows the number of pixels that are different between the two images. There are  pixels in the image, so the third column shows the percent of overall image pixels that are different. The maximum and arithmetic mean error are shown in the last two columns. Recall that our output images are 256 gray scale PNG files; the magnitude of error is given by
pixels in the image, so the third column shows the percent of overall image pixels that are different. The maximum and arithmetic mean error are shown in the last two columns. Recall that our output images are 256 gray scale PNG files; the magnitude of error is given by  .
.
Again, errors can be attributed to the difference in the computed width of the radar beam between the software and hardware programs. For comparison, a version of each program was written that does not include the  function and instead assumes that every projection contributes to every pixel (i.e., an infinite beamwidth). In this case, the images are almost identical; the number of errors drops to 0.1%, and the maximum error is 1. Thus, the error is not due to quantization of processed data; the computation of the radar beamwidth is responsible.
function and instead assumes that every projection contributes to every pixel (i.e., an infinite beamwidth). In this case, the images are almost identical; the number of errors drops to 0.1%, and the maximum error is 1. Thus, the error is not due to quantization of processed data; the computation of the radar beamwidth is responsible.
5.2.3. Multinode Performance
The second experiment involves running backprojection on multiple nodes simultaneously, using the MPI library to coordinate. These results show how well the application scales due to coarse-grained parallelism, that is, the speedup that can be gained by dividing a large problems into smaller pieces and running each piece separately. For this experiment, we create an output target image that is 64 times the size of the image created by a single node. Thus, when run on one node, 64 iterations are required; for two nodes, 32 iterations are required, and so on. Table 4 shows the results for a single dataset.
For both the software and hardware programs, five trials were run. For each trial, the time required to run backprojection and form the resulting image on each node was measured, and the maximum time reported. Thus, the overall run time is equal to the run time of the slowest node. The arithmetic mean of the times (in seconds) from the five trials are presented, with standard deviation. The mean run time is compared to the mean run time for one node in order to show the speedup factor.
Results are not presented for a 16-node trial of the hardware program. During our testing, it was not possible to find 16 nodes of the HHPC that were all capable of running the hardware program at once. This was due to hardware errors on some nodes, and inconsistent system software installations on others.
The mostly linear distribution of the data in Table 4 shows that for the backprojection application, we have achieved a nearly ideal parallelization. This can be attributed to the lack of data passing between nodes, combined with an insignificant amount of overhead involved in running the application in parallel with MPI. The hardware program shows a similar curve, except for  nodes, where the speedup drops off slightly. At run times under five seconds, the MPI overhead involved in synchronizing the nodes between each processing iteration becomes significant, resulting in a slight slowdown (6x speedup compared to the ideal 8x).
nodes, where the speedup drops off slightly. At run times under five seconds, the MPI overhead involved in synchronizing the nodes between each processing iteration becomes significant, resulting in a slight slowdown (6x speedup compared to the ideal 8x).
The speedup provided by the hardware program is further described in Table 5. Compared to one node running the hardware program, we have already seen the nearly linear speedup. Compared to an equal number of nodes running the software program, the hardware consistently performs around 75x faster. Again, for  , there is a slight drop off in speedup owing to the MPI overhead for short run times. Finally, we show that when compared to a single node running the software program, the combination of fine- and coarse-grained parallelism results in a very large performance gain.
, there is a slight drop off in speedup owing to the MPI overhead for short run times. Finally, we show that when compared to a single node running the software program, the combination of fine- and coarse-grained parallelism results in a very large performance gain.
6. Discussion
The results from Section 5.2.3 show that excellent speedup can be achieved by implementing the backprojection algorithm on an HPRC machine. As HPRC architectures improve and more applications are developed for them, designers will continue to search for ways to carve out more and more performance. Based on the lessons learned in Section 3 and our work on backprojection, in this section we suggest some directions for future research.
6.1. Future Backprojection Work
This project was developed with an eye toward implementation as a part of the Swathbuckler SAR system (see Section 4.1.2). Owing to the classified nature of that project, additional work beyond the scope of this project is required to integrate our backprojection implementation into that project. To determine the success of this aspect of the project, we would need to compare backprojection to the current Swathbuckler image formation algorithm, both in terms of run time as well as image quality.
Despite excellent speedup results, there are further avenues for improvement of our hardware. The Wildstar II boards feature two identical FPGAs, so it may be possible to process two images at once. If the data transfer to one FPGA can be overlapped with computation on the other, significant speedup is possible. It may also be possible for each FPGA to create a larger target image using more of the on-board SRAMs.
An interesting study could be performed by porting backprojection to several other HPRC systems, some of which can be targeted by high-level design languages. This would be the first step toward developing a benchmark suite for testing HPRC systems; however, without significant tool support-to-support application portability between HPRC platforms, this process would be daunting.
6.2. HPRC Systems and Applications
One common theme among the FPGA applications mentioned in Section 3 is data transfer. Applications that require a large amount of data to be moved between the host and the FPGA can eliminate most of the gains provided by increased parallelism. Backprojection does not suffer from this problem because the amount of parallelism exploited is so high that the data transfer is a relatively small portion of the run time, and some of the data transfers can be overlapped with computation. These are common and well-known techniques in HPRC application design.
This leads us to two conclusions. First, when considering porting an application to an HPRC system, it is important to consider whether the amount of available parallelism is sufficient to provide good speedup. Tools that can analyze an application to aid designers in making this decision are not generally available.
Second, it is crucial for the speed of the data transfers to be as high as possible. Early HPRC systems such as the HHPC use common bus architectures like PCI, which do not provide very high bandwidth. This limits the effectiveness of many applications. More recent systems such as the SRC-7 have included significantly higher bandwidth interconnect, leading to improved data transfer performance and increasing the number of applications that can be successfully ported. Designers of future HPRC systems must continue to focus on ways to improve the speed of these data transfers.
It is also noteworthy that the backprojection application presented here was developed using hand-coded VHDL, with some functional units from the Xilinx CoreGen library [30]. Writing applications in an HDL provides the highest amount of flexibility and customization, which generally implies the highest amount of exploited parallelism. However, HDL development time tends to be prohibitively high. Recent research has focused on creating programming languages and tools that can be used to increase programmer productivity, but applications developed with these tools have not provided speedups comparable to those of hand-coded HDL applications. The HPRC community would benefit from the continued improvement of development tools such as these.
Finally, each HPRC system has its own programming method that is generally incompatible with other systems. The standardization of programming interfaces would make the development of design tools easier, and would also increase application developer productivity when moving from one machine to the next. Alternately, tools to support portability of HPRC applications such as the VForce project [18] would also help HPRC developers.
7. Conclusions
In conclusion, we have shown that backprojection is an excellent choice for porting to an HPRC system. Through the design and implementation of this application, we have explored the benefits and difficulties of HPRC systems in general, and identified several important features of both these systems and applications that are candidates for porting. Backprojection is an example of the class of problems that demand larger amounts of computational resources than can be provided by desktop or single-node computers. As HPRC systems and tools mature, they will continue to help in meeting this demand and making new categories of problems tractable.
References
Cordes B: Parallel backprojection: a case study in high-performance reconfigurable computing, M.S. thesis. Department of Electrical and Computer Engineering, Northeastern University, Boston, Mass, USA; 2008.
Soumekh M: Synthetic Aperture Radar Signal Processing with MATLAB Algorithms. John Wiley & Sons, New York, NY, USA; 1999.
Kak AC, Slaney M: Principles of Computerized Tomographic Imaging. IEEE Press, New York, NY, USA; 1988.
Ross VW: Heterogeneous high performance computer. Proceedings of the High Performance Computing Modernization Program Users Group Conference (HPCMP '05), June 2005, Nashville, Tenn, USA 304-307.
High Performance Technologies Inc Cluster Computing, January 2008, http://www.hpti.com/ Cluster Computing, January 2008,
Annapolis Microsystems, Inc CoreFire FPGA Design Suite, January 2008, http://www.annapmicro.com/corefire.html CoreFire FPGA Design Suite, January 2008,
Coric S, Leeser M, Miller E, Trepanier M: Parallel-beam backprojection: an FPGA implementation optimized for medical imaging. Proceedings of the 10th ACM/SIGDA International Sysmposium on Field-Programmable Gate Arrays (FPGA '02), February 2002, Monterey, Calif, USA 217-226.
Gac N, Mancini S, Desvignes M: Hardware/software 2D-3D backprojection on a SoPC platform. Proceedings of the ACM Symposium on Applied Computing (SAC '06), April 2006, Dijon, France 222-228.
Xue X, Cheryauka A, Tubbs D: Acceleration of fluoro-CT reconstruction for a mobile C-arm on GPU and FPGA hardware: a simulation study. In Medical Imaging 2006: Physics of Medical Imaging, February 2006, San Diego, Calif, USA, Proceedings of SPIE Edited by: Flynn MJ, Hsieh J. 6142: 1494-1501.
Bockenbach O, Knaup M, Kachelrieß M: Implementation of a cone-beam backprojection algorithm on the cell broadband engine processor. Medical Imaging 2007: Physics of Medical Imaging, February 2007, San Diego, Calif, USA, Proceedings of SPIE 6510: 1-10.
Nguyen L, Ressler M, Wong D, Soumekh M: Enhancement of backprojection SAR imagery using digital spotlighting preprocessing. Proceedings of the IEEE Radar Conference, April 2004, Philadelphia, Pa, USA 53-58.
Hast A, Johansson L: Fast factorized back-projection in an FPGA, M.S. thesis. Halmstad University, Halmstad, Sweden; 2006. http://hdl.handle.net/2082/576
Ahlander A, Hellsten H, Lind K, Lindgren J, Svensson B: Architectural challenges in memory-intensive, real-time image forming. Proceedings of the 36th International Conference on Parallel Processing (ICPP '07), September 2007, Xian, China 35.
El-Ghazawi E, El-Araby E, Agarwal A, LeMoigne J, Gaj K: Wavelet spectral dimension reduction of hyperspectral imagery on a reconfigurable computer. Proceedings of the International Conference on Military and Aerospace Programmable Logic Devices (MAPLD '04), September 2004, Washington, DC, USA
Alam SR, Agarwal PK, Smith MC, Vetter JS, Caliga D: Using FPGA devices to accelerate biomolecular simulations. Computer 2007,40(3):66-73.
Meredith JS, Alam SR, Vetter JS: Analysis of a computational biology simulation technique on emerging processing architectures. Proceedings of the 21st International Parallel and Distributed Processing Symposium (IPDPS '07), March 2007, Long Beach, Calif, USA 1-8.
Tripp JL, Gokhale MB, Hansson AA: A case study of hardware/software partitioning of traffic simulation on the cray XD1. IEEE Transactions on Very Large Scale Integration (VLSI) Systems 2008,16(1):66-74.
Moore N, Conti A, Leeser M, King LS: Vforce: an extensible framework for reconfigurable supercomputing. Computer 2007,40(3):39-49.
Wang X, Braganza S, Leeser M: Advanced components in the variable precision floating-point library. Proceedings of the 14th Annual IEEE Symposium on Field-Programmable Custom Computing Machines (FCCM '06), April 2006, Napa, Calif, USA 249-258.
Underwood KD, Hemmert KS, Ulmer C: Architectures and APIs: assessing requirements for delivering FPGA performance to applications. Proceedings of the ACM/IEEE Conference on Supercomputing (SC '06), November 2006, Tampa, Fla, USA
Smith MC, Vetter JS, Alam SR: Scientific computing beyond CPUs: FPGA implementations of common scientific kernels. Proceedings of the 8th International Conference on Military and Aerospace Programmable Logic Devices (MAPLD '05), September 2005, Washington, DC, USA
Zhuo L, Prasanna VK: High performance linear algebra operations on reconfigurable systems. In Proceedings of the ACM/IEEE Conference on Supercomputing (SC '05), November 2005, Seatle, Wash, USA. IEEE Computer Society; 2.
Gokhale M, Rickett C, Tripp JL, Hsu C, Scrofano R: Promises and pitfalls of reconfigurable supercomputing. Proceedings of the International Conference on Engineering of Reconfigurable Systems and Algorithms (ERSA '06), June 2006, Las Vegas, Nev, USA 11-20.
Herbordt MC, VanCourt T, Gu Y, et al.: Achieving high performance with FPGA-based computing. Computer 2007,40(3):50-57.
Eugster PTh, Felber PA, Guerraoui R, Kermarrec A-M: The many faces of publish/subscribe. ACM Computing Surveys 2003,35(2):114-131. 10.1145/857076.857078
Rouse S, Bosworth D, Jackson A: Swathbuckler wide area SAR processing front end. Proceedings of the IEEE Radar Conference, April 2006, New York, NY, USA 1-6.
Linderman RW: Swathbuckler: wide swath SAR system architecture. Proceedings of the IEEE Radar Conference, April 2006, Verona, NY, USA 465-470.
Tucker S, Vienneau R, Corner J, Linderman RW: Swathbuckler: HPC processing and information exploitation. Proceedings of the IEEE Radar Conference, April 2006, New York, NY, USA 710-717.
GTK+ Project, March 2008, http://www.gtk.org/
Xilinx, Inc CORE Generator, March 2008, http://www.xilinx.com/products/design_tools/logic_design/design_entry/coregenerator.htm CORE Generator, March 2008,
Argonne National Laboratories MPICH, March 2008, http://www.mcs.anl.gov/research/projects/mpich2/ MPICH, March 2008,
Acknowledgments
This work was supported in part by the Center for Subsurface Sensing and Imaging Systems (CenSSIS) under the Engineering Research Centers Program of the National Science Foundation (Award no. EEC-9986821) and by the DOD High Performance Computer Modernization Program. The authors would also like to thank Dr. Richard Linderman and Prof. Eric Miller for their input to this project as well as Xilinx and Synplicity Corporations for their generous donations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cordes, B., Leeser, M. Parallel Backprojection: A Case Study in High-Performance Reconfigurable Computing. J Embedded Systems 2009, 727965 (2009). https://doi.org/10.1155/2009/727965
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/727965

 to pixel
to pixel 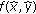 is not dependent on the contributions from all other projections
is not dependent on the contributions from all other projections  to that same pixel
to that same pixel  .
. to pixel
to pixel 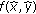 is not dependent on the contribution from
is not dependent on the contribution from  to all other pixels
to all other pixels 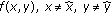 .
.

